Speeds
The calculation of reference speeds is standardised in ISO 15312. The stated reference speeds have been calculated in accordance with this standard.
Limiting speed
The limiting speed nG is based on practical experience and takes account of additional criteria such as smooth running, sealing function and centrifugal forces.
The limiting speeds indicated in the product tables must not be exceeded even under favourable operating conditions without prior consultation with Schaeffler.
Thermal speed rating
nϑr is used to calculate nϑ
The thermal speed rating nϑr is used as an ancillary value when calculating the thermally safe operating speed nϑ. This is the speed at which, under defined reference conditions, a bearing operating temperature of +70 °C is achieved.
The thermal speed rating is not a speed limit for the application of a bearing. It is primarily for the purpose of comparing the speed suitability of different bearing types under defined reference conditions.
A speed limit taking account of the thermal balance can be calculated using the thermally safe operating speed.
Reference conditions
The reference conditions are based on the usual operating conditions of the most significant bearing types and sizes.
They are defined as follows in ISO 15312:
- mean ambient temperature ϑAr = +20 °C
- mean bearing temperature at the outer ring ϑr = +70 °C
- load on radial bearings P1r = 0,05 · C0r
- load on axial bearings P1r = 0,02 · C0a
- the operating viscosities (axial bearings in accordance with DIN 732-1). These are selected for radial bearings such that similar reference speeds are achieved for both oil and grease lubrication
- radial bearings: 12 mm2/s (ISO VG 32)
- axial spherical roller bearings: 24 mm2/s (ISO VG 68)
- axial cylindrical roller bearings and axial needle roller bearings: 48 mm2/s (ISO VG 220)
- heat dissipation via the bearing seating surfaces ➤ Equation to ➤ Equation:
for radial bearings, bearing seat Ar ≦ 50 000 mm2 ➤ Equation:
Heat flow density
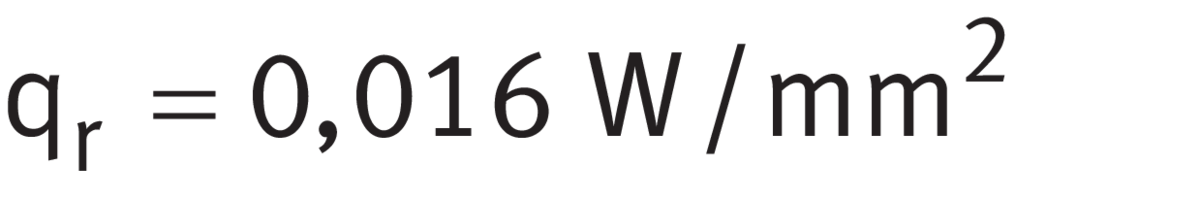
for radial bearings, bearing seat Ar > 50 000 mm2 ➤ Equation:
Heat flow density
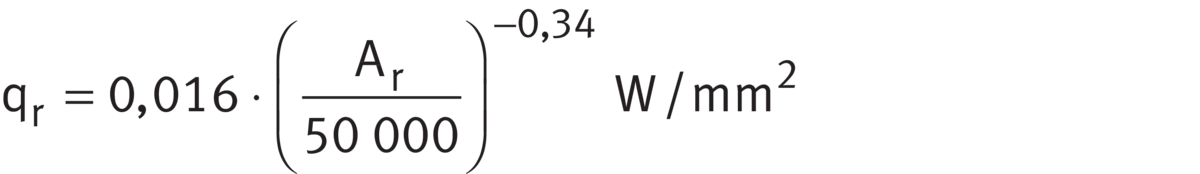
for axial bearings, bearing seat Ar ≦ 50 000 mm2 ➤ Equation:
Heat flow density
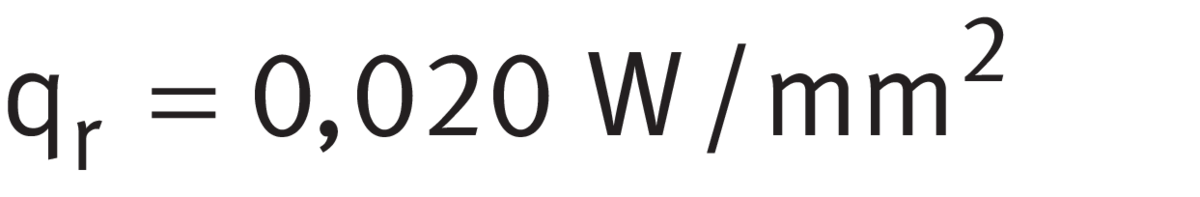
for axial bearings, bearing seat Ar > 50 000 mm2 ➤ Equation:
Heat flow density
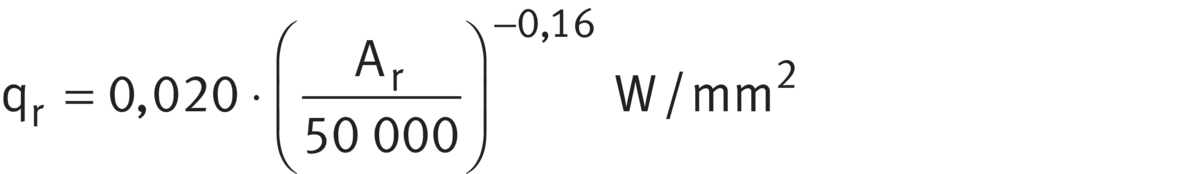
Thermally safe operating speed
The thermally safe operating speed nϑ is calculated in accordance with DIN 732:2010. The basis for the calculation is the heat balance in the bearing, the equilibrium between the frictional energy as a function of speed and the heat dissipation as a function of temperature. When conditions are in equilibrium, the bearing temperature is constant.
Preconditions for calculation
The permissible operating temperature determines the thermally safe operating speed nϑ of the bearing. The preconditions for calculation are correct mounting, normal operating clearance and constant operating conditions.
Calculation not applicable
The calculation method is not valid for:
- sealed bearings with contact seals, since the maximum speed is restricted by the permissible sliding speed at the seal lip
- yoke and stud type track rollers
- aligning needle roller bearings
- axial deep groove and axial angular contact ball bearings
Limiting speed nG
The limiting speed nG must always be observed.
Calculate thermally safe operating speed
Calculation of frictional power
The equilibrium between the frictional power and heat dissipation is given in ➤ Equation and ➤ Equation. For an explanation of the parameters ➤ Equation.
Frictional power
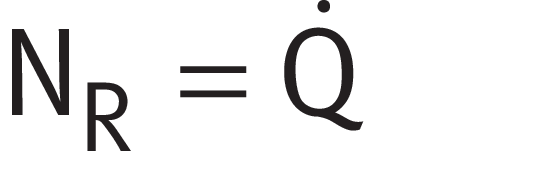
Frictional power
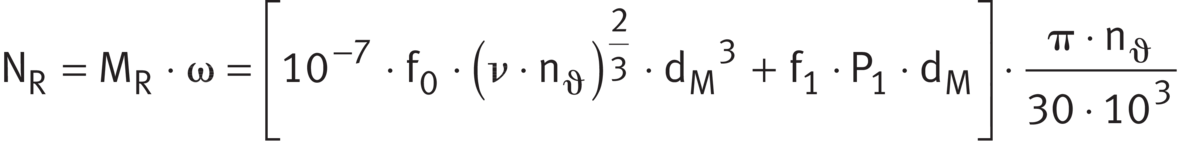
Heat flow
The total dissipated heat flow  is calculated in accordance with ➤ Equation.
is calculated in accordance with ➤ Equation.
Total dissipated heat flow
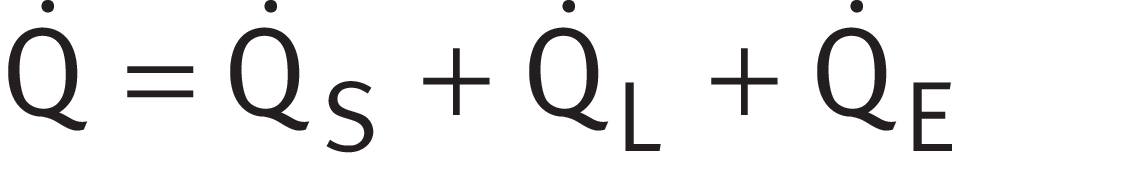
According to ➤ Equation, frictional power is equal to the dissipated heat flow.
Frictional power = dissipated heat flow
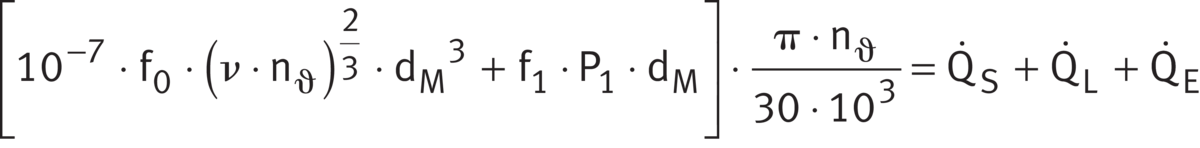
Lubricant film parameter KL
➤ Equation can only be solved iteratively. The introduction of the lubricant film parameter KL, the load parameter KP and the speed ratio fn has made this more manageable ➤ Equation.
Lubricant film parameter
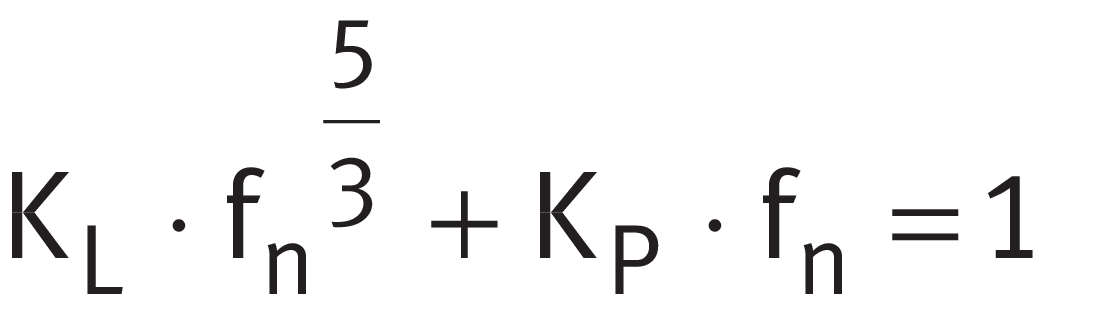
Speed ratio fn
In the normal operating range of 0,01 ≦ KL ≦ 10 and 0,01 ≦ KP ≦ 10, fn can be calculated in accordance with ➤ Equation and ➤ Figure.
Speed ratio
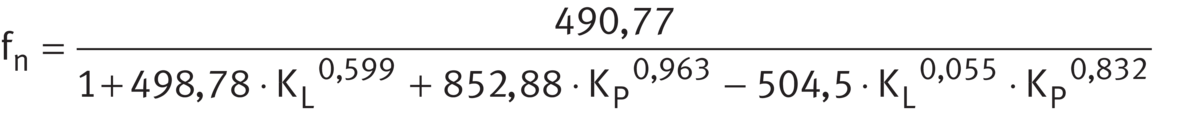
Thermally safe operating speed
The thermally safe operating speed nϑ is calculated by multiplying the thermal speed rating nϑr by the factor for thermal speed ratio fn ➤ Equation.
Thermally safe operating speed
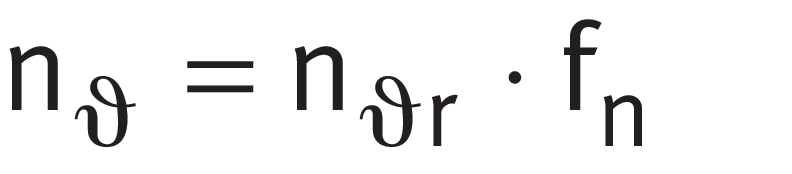
Heat dissipation via the bearing seating surfaces
Heat dissipation via the bearing seating surfaces is calculated in accordance with ➤ Equation.
Heat dissipation via the bearing seating surfaces
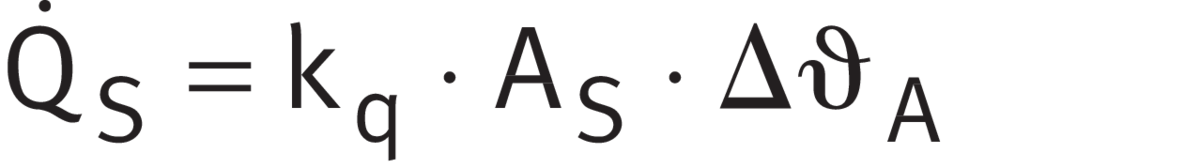
Heat dissipation via the lubricant
Heat dissipation via the lubricant is calculated in accordance with ➤ Equation.Heat dissipation via the lubricant
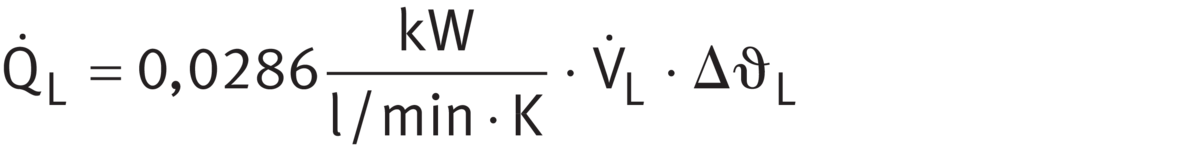
Lubricant film parameter KL
The lubricant film parameter KL is calculated in accordance with ➤ Equation.
Lubricant film parameter
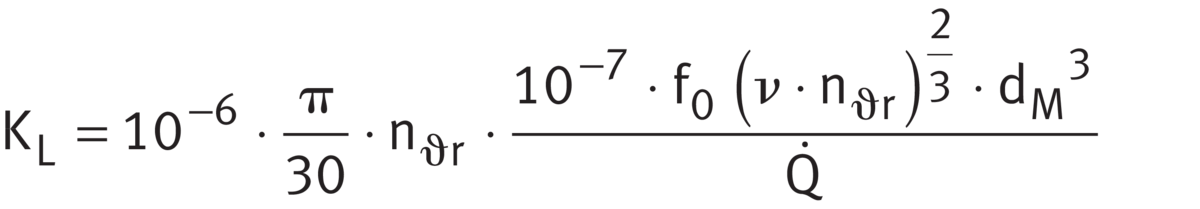
Load parameter KP
The load parameter KP is calculated in accordance with ➤ Equation.
Load parameter
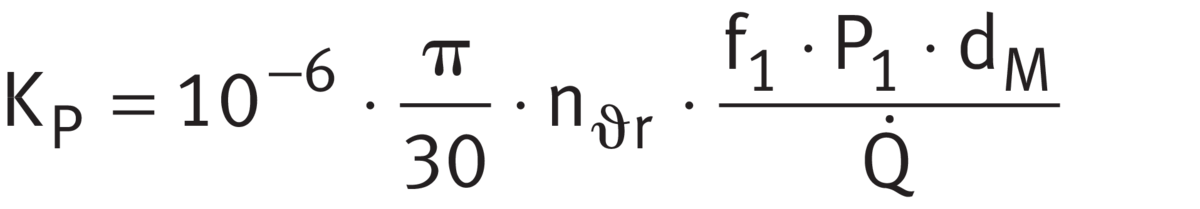
Legend
| NR | W |
Frictional power |
 |
kW |
Total dissipated heat flow |
| MR | Nmm |
Total frictional torque |
| f0 | - |
Bearing factor for frictional torque as a function of speed |
| ν | mm2/s |
Kinematic viscosity of the lubricant at operating temperature |
| nϑ | min-1 |
Thermally safe operating speed |
| dM | mm |
Mean bearing diameter (D + d)/2 |
| f1 | - |
Bearing factor for frictional torque as a function of load |
| P1 | N |
Decisive load: radial load for radial bearings, axial load for axial bearings. |
 S S |
kW |
Heat flow dissipated via the bearing seating surfaces |
 L L |
kW |
Heat flow dissipated by the lubricant |
 E E |
kW |
Heat flow. For heating by external source (+), for cooling by external source (–) |
| KL | - |
Lubricant film parameter |
| fn | - |
Speed ratio |
| KP | - |
Load parameter |
| nϑr | min-1 |
Thermal speed rating; see product tables |
| kq | 10-6 kW/ (mm2 · K) |
Heat transfer coefficient, as a function of the bearing seating surface ➤ Figure. This is dependent on the housing design and size, the housing material and the installation position. |
Legend (continuation)
| AS | mm2 |
Heat-dissipating bearing seating surface |
| ΔϑA | K |
Difference between mean bearing temperature and ambient temperature |
 L L |
l/min |
Oil flow |
| ΔϑL | K |
Difference between oil inlet temperature and oil outlet temperature |
| B | mm |
Bearing width |
| d | mm |
Bearing bore diameter |
| D | mm |
Bearing outside diameter |
| d1 | mm |
Outside diameter of shaft locating washer |
| D1 | mm |
Inside diameter of housing locating washer |
| T | mm |
Total width of tapered roller bearing |
|
Speed ratio fn as a function of lubricant film fn = speed ratio KL = lubricant film parameter KP = load parameter |
 |
|
Heat transfer coefficient kqas a function of the bearing seating surface kq = heat transfer coefficient, as a function of the bearing seating surface AS = heat-dissipating bearing seating surface
|
 |





